Hash Maps with Insertion Ordering

When programming, the map data structure is quite handy. When I first used Perl, the thing that struck me the most was how simple it was to use hashes, as they are called. They came in handy for everything! Map is also a major element of Go; it is one of the built-in object types that supports syntax and generics. I believe that the majority of Python programmers have had a similar experience. They are referred to as dictionaries, and they are ubiquitous. Each object in JavaScript is also a hash map. When I worked on V8, we had to go to great efforts to conceal the performance implications of that choice, but I am still a supporter of easy-to-use hash maps in programming languages.
However, all of these languages began with unordered hash maps. You can store all of your key-value pairs in the hash map, but when you try to traverse the contents of the map, they are returned in an odd order. It is not the order in which you placed them, and it is probably definitely not the order in which you desired. Go and Perl opted to address this by increasing the randomness of hash ordering. JavaScript and Python used the opposite approach and changed the ordering to match the order of insertion. (There is one exception in the case of JS objects: numeric property names are ordered numerically, not in order of insertion.) That one drew a lot of ire on V8’s bug tracker!)
The most efficient way to create hash maps that are insertion ordered is to use a variant of what Python refers to as a “compact dictionary,” which was popularized/rediscovered by Raymond Hettinger. (According to Hettinger, there is previous work, implemented in Java, that is similar to the internal object implementation of V8, which was devised by Lars Bak, another Toit co-founder.) In compact dictionaries, the keys and values are stored in a linear array, and the linear array is indexed by a more standard open addressing hash table. It appears as follows.
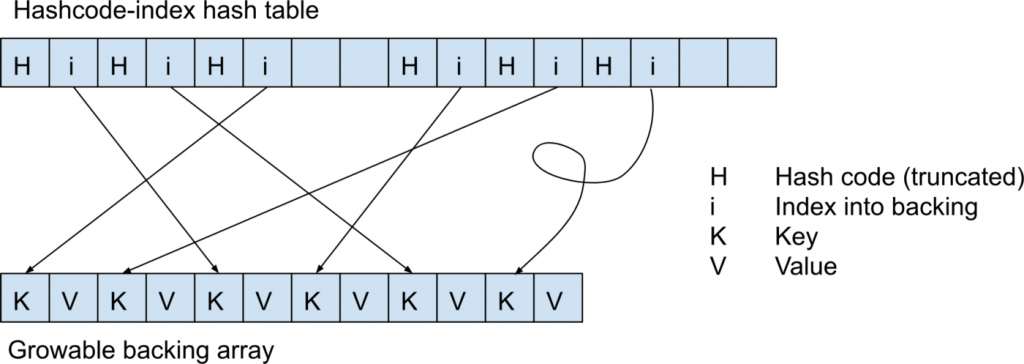
This is also how a hash map appears in Toit. Indeed, hash numbers in the index table are not required, but they speed up lookup. Storing the final few bits of the hash code enables us to discover the majority of index collisions without examining the keys in the underlying array. Additionally, having hash codes in the index speeds up the process of rebuilding the index when it grows too large.
If a user deletes an entry from this type of hash map, we change the key with a marker indicating that the entry was deleted. Perhaps disturbingly, we refer to these markings as “tombstones.” When there are sufficient of these tombstones, the hash map is recreated, which is acceptable. This has no effect on your average speed due to the magic of amortised constant time.
This is fantastic because it now provides an efficient method for creating hash maps with insertion ordering. These are non-aggressive hash maps, which is why we utilised them in the Dart project as well, which is now probably best known as the engine powering Flutter. (Several of the Dart founders later founded Toit.)
Additional indicators that your hash maps do not despise you
The other feature that you will immediately require is the ability to utilise any object as a key in a hash map. In languages that do not support this (Perl, Python, Go, and JavaScript until recently), you can use strings as keys, with each key object generating a unique string. This is not very elegant, as your programme generates a large number of strings that were not required.
A step up in sophistication is the ability to specify the equality function for the keys in a map. For example, in Java and Toit, you can provide a custom equals function for the class of a collection’s keys. By contrast, JavaScript’s map implementation makes no use of object identity. You cannot create a new item and then check to see if an object with an equivalent key already exists in the map. Again, the inelegant approach requires that each generate strings and use them as keys.
Additionally, it is occasionally essential to declare the equality function per map rather than per key type. In C++, this is accomplished using the Hash and Pred template parameters on unordered map. (However, as the name unordered map implies, conventional C++ collections despise you, and hence this additional feature provides no consolation.) At the moment, Toit does not provide per-map equality functions, but this will change shortly! In Java, you would need to encapsulate the keys in your map or use Trove.
The thorn in the side of the ointment and how to remove it
Even if your language has compact dictionaries, there is a slight kink in the works. Your hash maps will continue to act as though they despise you in certain scenarios, but in a different way! Certain individuals prefer to utilise hash maps (and sets, which implement the same concept) as a deduplicating work queue. You can add “tasks” to the set, and because it is a set, it will automatically disregard duplicates. A task queue (also known as a FIFO queue) requires both an append-to-the-end and a remove-from-the-start operation. We already have the append-to-the-end action, and it is simple to perform a remove-first operation by inspecting the beginning of the backing array. If the Toit language does not already include this function, the following could be added:
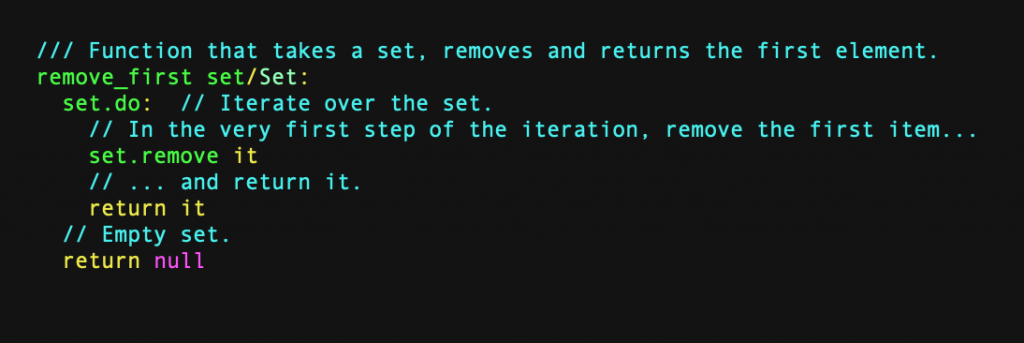

The problem arises after a while of using a set or map like this. There will be a lot of tombstones near the start of the backing, and suddenly the remove-from-the-start operation isn’t so fast. It needs to skip over more and more tombstones, and the run time to insert-then-remove n items becomes quadratic. This issue can’t be solved by rebuilding the hash map more frequently, because if you do that, you lose the property of amortized constant time operations.
An ad-hoc solution would be to record for each hash map where the first entry is in the backing array. This feels like a band-aid though. What if users want to repeatedly remove the last entry using a set as a sort of deduplicating stack (or LIFO)? The hateful quadratic hash map problem would be back. What if they want to repeatedly remove the second entry in the set? One thing I learned on V8 is that it’s hard to predict what your users will do with a programming language implementation you have built.
And we built Toit to work on tiny devices. Do we really want to spend an extra word per hash map to record the number of leading tombstones? The solution we came up with was tombstones with distance markers. Each tombstone additionally records the distance to the next real entry, either on the left or the right. We update this lazily when scanning through the backing, so it doesn’t cost any time on other operations, but it lets us skip long stretches of tombstones wherever they appear.

For the common case where there are no deletions, or the deletions are randomly distributed, nothing changes, but for the problematic cases we retain the desirable property of amortized constant time insertion and deletion.
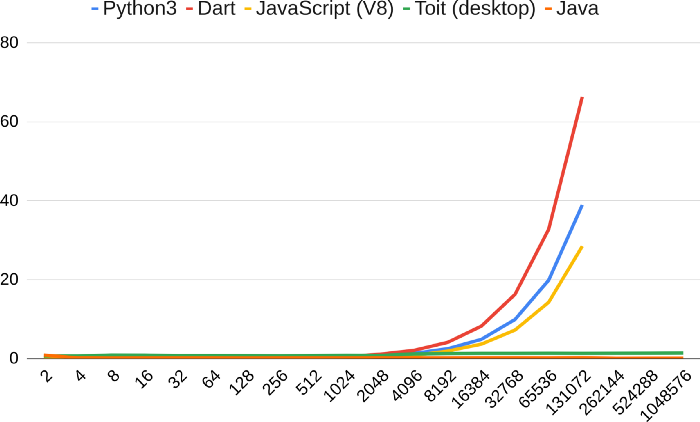
Testing Languages for this Bug
I wrote a tiny program to test whether language implementations have quadratic slowdowns when using a set as a FIFO. I’m only testing languages that have an insertion-ordered set. For JavaScript I’m using the new(ish) Set, rather than abusing ordinary objects as hash maps. In Java I used LinkedHashMap, which has a completely different internal representation. I suspect LinkedHashMap of being fairly profligate in memory use (I’ll be blogging about this issue soon), but it’s the fastest insertion ordered set I tested, especially when the adaptive JIT kicks in.
So here, for your enjoyment, is the graph for various languages. Currently, all the compact-dictionary-based implementations (except Toit) have this issue. Hopefully, this blog post will inspire the implementers to fix it.